தேனீக்கள் மற்றும் குளவிகளுக்கான The bees and wasps கட்டிடக்கலை சிக்கல்களை வடிவியல் எவ்வாறு தீர்க்கிறது!

தேனீக்கள் மற்றும் மஞ்சள் நிற (The bees and wasps) ஜாக்கெட்டுகள் கணிதவியலாளர்களைப் போல் இல்லை. ஆனால் கூட்டாக, பூச்சிகள் ஒரு பொதுவான கட்டடக்கலை புதிரை ஒரு வடிவியல் தீர்வைப் பயன்படுத்தி தீர்க்க முடியும். அவை ஒருவருக்கொருவர் சுயாதீனமாக உருவாகின்றன.

அவற்றின் காலனிகள் வளரும்போது, இந்த தேனீக்கள் மற்றும் குளவிகள் இறுதியில் அவற்றின் கூடுகளை உருவாக்கும் அறுகோண செல்களின் அளவை அதிகரிக்க வேண்டும். ஆனால் கூடு பொருள் விலை உயர்ந்தது. மேலும் வெவ்வேறு அளவிலான அறுகோணங்களை ஒரு தொடர்ச்சியான வரிசையில் திறமையாக இணைப்பது கடினம்.

தேனீக்கள் மற்றும் குளவிகள் இரண்டும் சில ஜோடி ஐந்து பக்க மற்றும் ஏழு பக்க செல்களில் கலந்து இந்த சிக்கலை தீர்த்துள்ளன. அவை ஆறு பக்க அறுகோணங்களின் வெவ்வேறு அளவுகளுக்கு இடையிலான இடைவெளியைக் குறைக்கின்றன, என்று ஆராய்ச்சியாளர்கள் தெரிவிக்கின்றனர். இந்த பிழைத்திருத்தம் இந்த சிக்கலுக்கான உகந்த தீர்வுக்கு அருகில் உள்ளது, என்று குழு கூறுகிறது.

“அறுகோண சீப்பு தேனீக்கள் மற்றும் குளவிகளின் பயன்பாடு மிகவும் திறமையான, நிலையான வடிவம் என்பதை நாங்கள் நீண்ட காலமாக அறிந்திருக்கிறோம்” என்று ஆய்வில் ஈடுபடாத ஏதென்ஸில் உள்ள ஜார்ஜியா பல்கலைக்கழகத்தின் தேனீ உயிரியலாளர் லூயிஸ் பார்ட்லெட் கூறுகிறார். ஆனால் வெவ்வேறு அளவிலான அறுகோணங்களை கலப்பது தந்திரமானது.

தேனீக்கள் மற்றும் சில குளவிகள் போன்ற சமூக பூச்சி காலனிகள், தங்கள் தாய் ராணியின் சந்ததிகளை வளர்க்கும் பெண் தொழிலாளர்களால் நடத்தப்படுகின்றன. தேனீக்கள் மெழுகிலிருந்தும் குளவிகள் காகிதத்திலிருந்தும் உருவாக்கும் அறுகோண செல்களில் இதைச் செய்கின்றன. அதன் வாழ்க்கைச் சுழற்சியின் ஒரு குறிப்பிட்ட கட்டத்தில், காலனியானது தொழிலாளர்களை வளர்ப்பதில் இருந்து ஆண் மற்றும் புதிய ராணிகள் போன்ற இனப்பெருக்கத்தை வளர்ப்பதற்கு மாற வேண்டும்.

இந்த இனப்பெருக்கம் பெரும்பாலும் தொழிலாளர்களை விட பெரியதாக இருக்கும். அதாவது அறுகோண செல்களும் பெரிதாக இருக்க வேண்டும். அலபாமாவில் உள்ள ஆபர்ன் பல்கலைக்கழகத்தின் உயிரியலாளர் மைக்கேல் ஸ்மித் கூறுகையில், உங்கள் குளியலறையின் தரையை யாரோ ஒருவர் டைல்ஸ் போடுவதை நினைத்துப் பாருங்கள்.

உங்களிடம் இரண்டு வெவ்வேறு அளவிலான அறுகோணங்கள் இருந்தால், சிறியவற்றை ஒருபுறமும் பெரியவற்றை மறுபுறமும் தொகுக்கப் போகிறீர்கள் என்றால், நீங்கள் அவற்றைப் பொருத்த முயற்சிக்கும் போது இயல்பாகவே உங்களுக்கு ஏதேனும் சிக்கல்கள் இருக்கும்.

தேனீக்கள் மற்றும் குளவிகள் இந்த டைலிங் புதிரை எவ்வாறு தீர்க்கின்றன என்பதைக் கண்டறிய, ஸ்மித்தும் சக ஊழியர்களும் ஐந்து வகையான தேனீக்களின் (Apis mellifera, A. cerana, A. dorsata, A. florea and A. Andreniformis), நான்கு வகையான வெஸ்புலாவின் காலனிகளின் 115 படங்களை ஆய்வு செய்தனர்.

குளவி (வி. வல்காரிஸ், வி. மாகுலிஃப்ரான்ஸ், வி. ஃபிளாவோபிலோசா மற்றும் வி. ஷிடாய்), பொதுவாக வட அமெரிக்காவில் மஞ்சள் ஜாக்கெட்டுகள் என்று அழைக்கப்படுகிறது. மேலும் ஒரு வகை காகித குளவி (மெட்டாபோலிபியா மீசோஅமெரிக்கா).

கார்னெல் பல்கலைக்கழகத்தின் ரோபோட்டிஸ்ட் குழு உறுப்பினர் கிர்ஸ்டின் பீட்டர்சன் உருவாக்கிய தானியங்கு பட பகுப்பாய்வு கருவியைப் பயன்படுத்தி, விஞ்ஞானிகள் 22,745 செல்களிலிருந்து செல் சுவர்களின் நீளம் மற்றும் ஒவ்வொரு செல்லின் அண்டை நாடுகளின் எண்ணிக்கை போன்ற தரவைப் பிரித்தெடுத்தனர். ஸ்மித் ஒவ்வொரு கலத்தின் தரவையும் கையால் சரிபார்த்தார். “நான் துரதிர்ஷ்டவசமான சாப்,” என்று அவர் கூறுகிறார்.

தானியங்கு கருவியானது, சரியான அறுகோணங்கள் இல்லாத ஒழுங்கற்ற செல்களிலிருந்து தரவைப் பெற குழுவை அனுமதித்தது. அவற்றை கைமுறையாக அளவிடுவதில் உள்ள சிரமம் காரணமாக பல விஞ்ஞானிகள் புறக்கணித்தனர். இந்த வெளித்தோற்றத்தில் தவறாக வடிவமைக்கப்பட்ட செல்கள் வேறு எதுவும் இல்லை.

சிறிய தொழிலாளர் உயிரணுக்களிலிருந்து பெரிய இனப்பெருக்க உயிரணுக்களுக்கு மாறும்போது, ​​அனைத்து தேனீக்களும் குளவிகளும் இடைவெளியைக் குறைக்க ஐந்து பக்க மற்றும் ஏழு பக்க செல்களை இணைக்கின்றன. ஐந்து-ஏழு இணைத்தல் ஒரு ஜோடி அறுகோணங்களின் அதே எண்ணிக்கையிலான திறந்த பக்கங்களைக் கொண்டுள்ளது.

இரண்டு வகையான இணைந்த ஜோடிகளும் மற்ற கலங்களுடன் இணைக்க 10 பக்கங்களைக் கொண்டுள்ளன. எனவே இது வடிவத்தை சீர்குலைக்காது. மேலும் ஏழு பக்க கலத்தின் பெரிய அளவு தேனீக்கள் மற்றும் குளவிகள் அதன் மறுபுறத்தில் பெரிய அறுகோணங்களை உருவாக்கத் தொடங்க அனுமதிக்கிறது. “அவர்கள் எப்போதும் ஐந்து பக்க கலத்தை முதலில் உருவாக்குகிறார்கள், பின்னர் ஏழு பக்க கலத்தை உருவாக்குகிறார்கள்” என்று ஸ்மித் கூறுகிறார்.

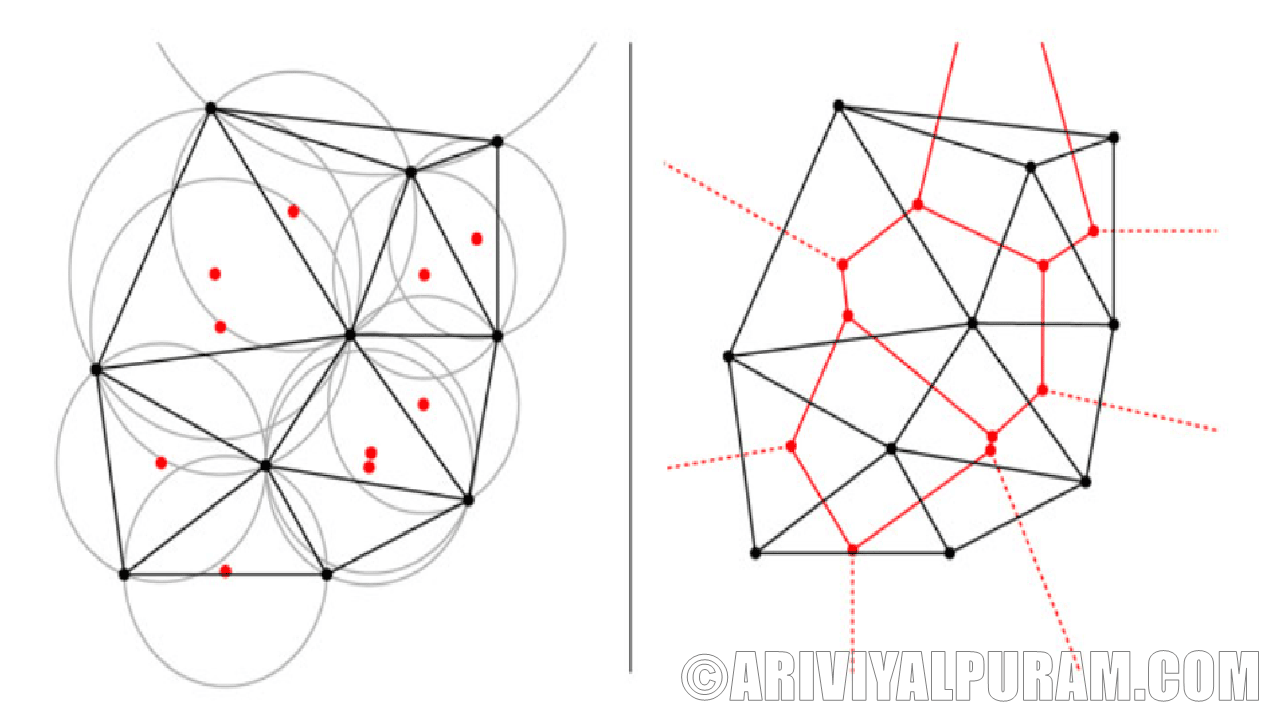
கார்னெல் பல்கலைக்கழகத்தின் கணினி விஞ்ஞானி நில்ஸ் நாப், இந்த உத்தியின் கணித மாதிரியை வடிவமைத்து, தேனீக்கள் மற்றும் குளவிகள் செய்வது உகந்த வடிவியல் தீர்வுக்கு அருகில் இருப்பதைக் கண்டறிந்தார். ஒரு தேனீ அல்லது குளவியை வளர்க்கும் அளவுக்கு ஒவ்வொரு உயிரணுவும் பெரியதாக இருக்கும் வகையில் வடிவங்களின் வரிசையை உருவாக்குவதற்கான மிகச் சிறந்த வழி டெலானே முக்கோணத்தால் குறிப்பிடப்படுகிறது.

டஜன் கணக்கான புள்ளிகளால் குறிக்கப்பட்ட ஒரு தாளை கற்பனை செய்து பாருங்கள். பின்னர், அண்டை புள்ளிகளை மட்டும் இணைப்பதன் மூலம் தாளை முக்கோணங்களுடன் நிரப்பவும். இறுதியாக, ஒவ்வொரு முக்கோணத்தையும் சுற்றி, ஒவ்வொரு மூலையையும் தொடும் ஒரு வட்டத்தை வரையவும். டெலானே முக்கோணத்தின் அமைப்பில் அந்த வட்டங்களில் எந்தப் புள்ளியும் இல்லை.

அண்டை வட்டங்களின் மையங்களை இணைக்கும் கூடுதல் கோடுகளை வரைவது, தேனீ மற்றும் குளவி கூடுகளில் காணப்படும் அறுகோணங்களின் பின்னல் போன்ற பலகோணங்களின் ஓடுகளை உருவாக்குகிறது. கூடுகளில் பெரிய அறுகோணங்களைச் சேர்ப்பது, முழு வரிசையையும் முழுமையடையாமல் மெதுவாக அங்குலமாக்குகிறது.

அதாவது இடைவெளிகள் உருவாகலாம் அல்லது கூட்டை ஒன்றாக வைத்திருக்க தொழிலாளர்கள் பயன்படுத்த முடியாத கலத்தை உருவாக்க வேண்டியிருக்கும், என்று Napp இன் மாதிரி காட்டுகிறது. Delaunay நிபந்தனை மீறப்படுவதைப் போலவே ஐந்து-ஏழு ஜோடியைச் சேர்ப்பதே உகந்த விஷயம். தேனீ மற்றும் குளவி இனங்கள் முழுவதும் அனைத்து அறுகோணமற்ற உயிரணுக்களில் சுமார் 85 சதவீதம் மாதிரி கணிப்பது போலவே ஐந்து-ஏழு ஜோடிகளில் உள்ளன.

இந்த ஆய்வில் பயன்படுத்தப்பட்ட தேனீக்கள் மற்றும் குளவிகள் 179 மில்லியன் ஆண்டுகால பரிணாம வளர்ச்சியால் பிரிக்கப்பட்டு வெவ்வேறு பொருட்களால் அவற்றின் கூடுகளை உருவாக்குகின்றன. “ஆனால் இருவரும் அறுகோண அளவுகளுக்கு இடையில் மாறுவதற்கு இந்த ஐந்து-ஏழு விதியைப் பயன்படுத்துவதற்கு பரிணமித்தனர்,” என்று பார்ட்லெட் கூறுகிறார். பரிணாமம் சவால்களை உகந்த முறையில் தீர்க்கும் போக்கைக் கொண்டுள்ளது.