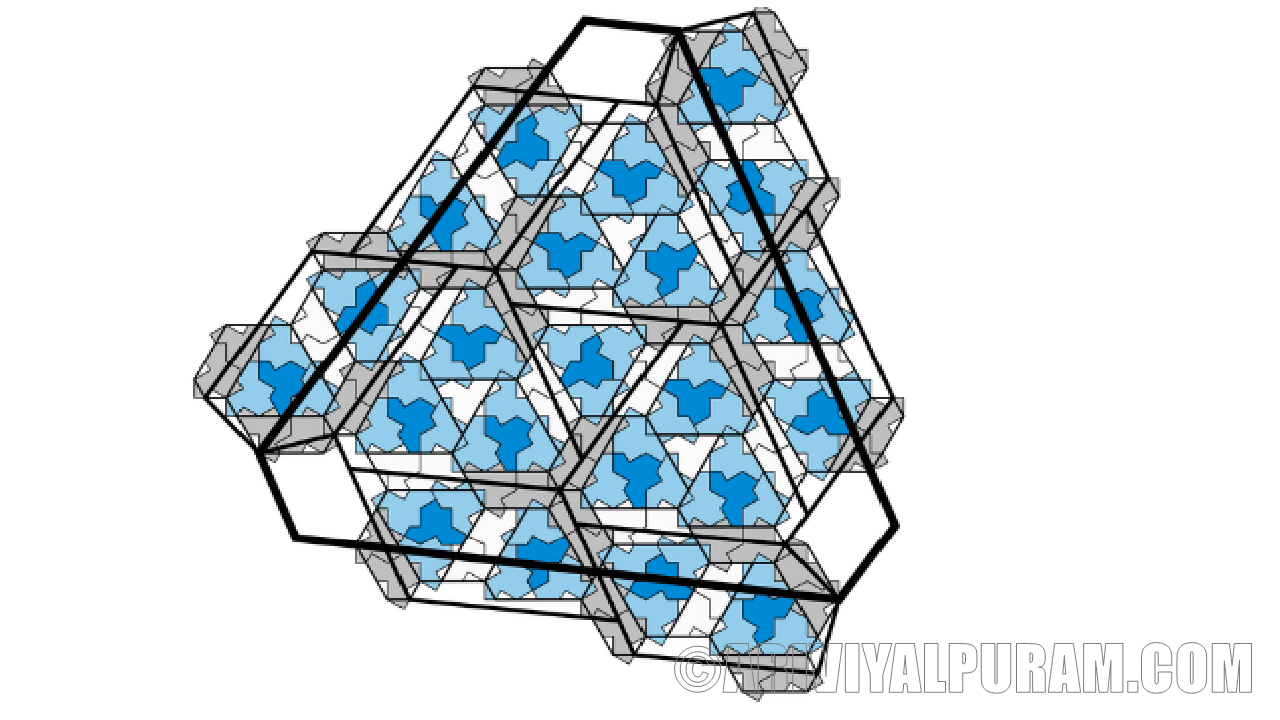
“தொப்பி” என்று அழைக்கப்படும் (Einstein) 13-பக்க வடிவமானது கணிதவியலாளர்கள் தங்கள் தொப்பிகளை சாய்த்து வைத்து கொண்டிருக்கும் அமைப்பில் இருக்கும்.
இது “ஐன்ஸ்டீனின்” முதல் உண்மையான உதாரணம், இது குளியலறையின் தரை ஓடுகளைப் போலவே, ஒரு விமானத்தின் ஒரு சிறப்பு டைலிங் உருவாக்கும் ஒற்றை வடிவமாகும். இது ஒரு முழு மேற்பரப்பையும் இடைவெளிகள் அல்லது ஒன்றுடன் ஒன்று இல்லாமல் மறைக்க முடியும், ஆனால் மீண்டும் மீண்டும் நிகழாத ஒரு வடிவத்துடன் மட்டுமே இது நிகழும்.
“எல்லோரும் ஆச்சரியப்படுகிறார்கள் மற்றும் மகிழ்ச்சியடைந்துள்ளனர்,” என்று கண்டுபிடிப்பில் ஈடுபடாத நார்தாம்ப்டன், மாஸில் உள்ள ஸ்மித் கல்லூரியின் கணிதவியலாளர் மார்ஜோரி செனெச்சால் கூறுகிறார். கணிதவியலாளர்கள் அரை நூற்றாண்டு காலமாக அத்தகைய வடிவத்தைத் தேடிக்கொண்டிருந்தனர். “இது போன்ற ஒரு விஷயம் இருக்க முடியும் என்பது கூட தெளிவாக இல்லை,” என்று செனெச்சல் கூறுகிறார்.
“ஐன்ஸ்டீன்” என்ற பெயர் சின்னமான இயற்பியலாளரைக் கற்பனை செய்தாலும், இது “ஒரு கல்” என்று பொருள்படும் ஜெர்மன் ஐன் ஸ்டெய்னிலிருந்து வந்தது, இது ஒற்றை ஓடுகளைக் குறிக்கிறது. ஐன்ஸ்டீன் ஒழுங்கிற்கும் இடையில் ஒரு வித்தியாசமான சுத்திகரிப்பு நிலையத்தில் அமர்ந்திருக்கிறார். ஓடுகள் ஒன்றாக நேர்த்தியாகப் பொருந்தினாலும், எல்லையற்ற விமானத்தை மறைக்க முடியும் என்றாலும், அவை அபிரியோடிக் ஆகும், அதாவது அவை மீண்டும் மீண்டும் ஒரு வடிவத்தை உருவாக்க முடியாது.
ஒரு குறிப்பிட்ட முறை மூலம், ஓடுகளை மாற்றுவது மற்றும் அவற்றின் முந்தைய ஏற்பாட்டுடன் சரியாகப் பொருந்துவது சாத்தியமாகும். எடுத்துக்காட்டாக, எல்லையற்ற செக்கர்போர்டு, வரிசைகளை இரண்டாக ஸ்லைடு செய்தால் ஒரே மாதிரியாக இருக்கும். மற்ற ஒற்றை ஓடுகளை அவ்வப்போது இல்லாத வடிவங்களில் ஏற்பாடு செய்வது சாத்தியம் என்றாலும், தொப்பி சிறப்பு வாய்ந்தது, ஏனெனில் அது ஒரு குறிப்பிட்ட கால வடிவத்தை உருவாக்க வழி இல்லை.
டேவிட் ஸ்மித், ஒரு தொழில்சார்ந்த கணிதவியலாளரால் அடையாளம் காணப்பட்டார், அவர் தன்னை “கற்பனையில் வடிவங்களை உருவாக்குபவர்” என்று வர்ணிக்கிறார் மற்றும் ஆன்லைனில் மார்ச் 20 அன்று arXiv.org இல் வெளியிடப்பட்ட ஒரு தாளில், தொப்பி ஒரு பாலிகைட் – சிறிய காத்தாடி வடிவங்கள் ஒன்றாக ஒட்டிக்கொண்டது. இது ஐன்ஸ்டீன்களுக்கான தேடலில் நெருக்கமாக ஆய்வு செய்யப்படாத ஒரு வகை வடிவம் என்று நியூயார்க் நகரில் உள்ள தேசிய கணித அருங்காட்சியகத்தைச் சேர்ந்த சைம் குட்மேன்-ஸ்ட்ராஸ் கூறுகிறார், பயிற்சி பெற்ற கணிதவியலாளர்கள் மற்றும் கணினி விஞ்ஞானிகளான ஸ்மித் இணைந்து ஆய்வு செய்த குழுவில் ஒருவர் தொப்பி.
இது ஒரு வியக்கத்தக்க எளிய பலகோணம். இந்த வேலைக்கு முன், ஐன்ஸ்டீன் எப்படி இருப்பார் என்று நீங்கள் கேட்டால், குட்மேன்-ஸ்ட்ராஸ் கூறுகிறார், “நான் சில பைத்தியக்காரத்தனமான, மோசமான விஷயங்களை வரைந்திருப்பேன்” என்கிறார்.
வெவ்வேறு வடிவங்களின் பல ஓடுகளை உள்ளடக்கிய மீண்டும் மீண்டும் செய்யாத டைலிங் பற்றி கணிதவியலாளர்கள் முன்பு அறிந்திருந்தனர். 1970 களில், கணிதவியலாளர் ரோஜர் பென்ரோஸ், இரண்டு வெவ்வேறு வடிவங்கள் கால இடைவெளியில் இல்லாத டைலிங் ஒன்றை உருவாக்குகின்றன என்பதைக் கண்டுபிடித்தார். அங்கிருந்து, “ஆச்சரியப்படுவது இயற்கையானது, இதைச் செய்யும் ஒரு ஓடு இருக்க முடியுமா?” ஆராய்ச்சியில் ஈடுபடாத வாஷிங்டன் போடெல் பல்கலைக்கழகத்தின் கணிதவியலாளர் கேசி மான் கூறுகிறார். அது இறுதியாக கண்டுபிடிக்கப்பட்டது, “இது மிகப்பெரியது.”
மற்ற வடிவங்கள் நெருங்கிவிட்டன. டெய்லர்-சோகோலார் டைல்ஸ் ஆபிரியோடிக், ஆனால் அவை பல துண்டிக்கப்பட்ட துண்டுகளின் குழப்பம் – பெரும்பாலான மக்கள் ஒற்றை ஓடு என்று நினைப்பதில்லை. “நட்சத்திரங்கள் இல்லாத முதல் தீர்வு இதுவாகும்” என்று CNRS இன் கணிதவியலாளர் மைக்கேல் ராவ் மற்றும் பிரான்சில் École Normale Superieure de Lyon கூறுகிறார்கள்.
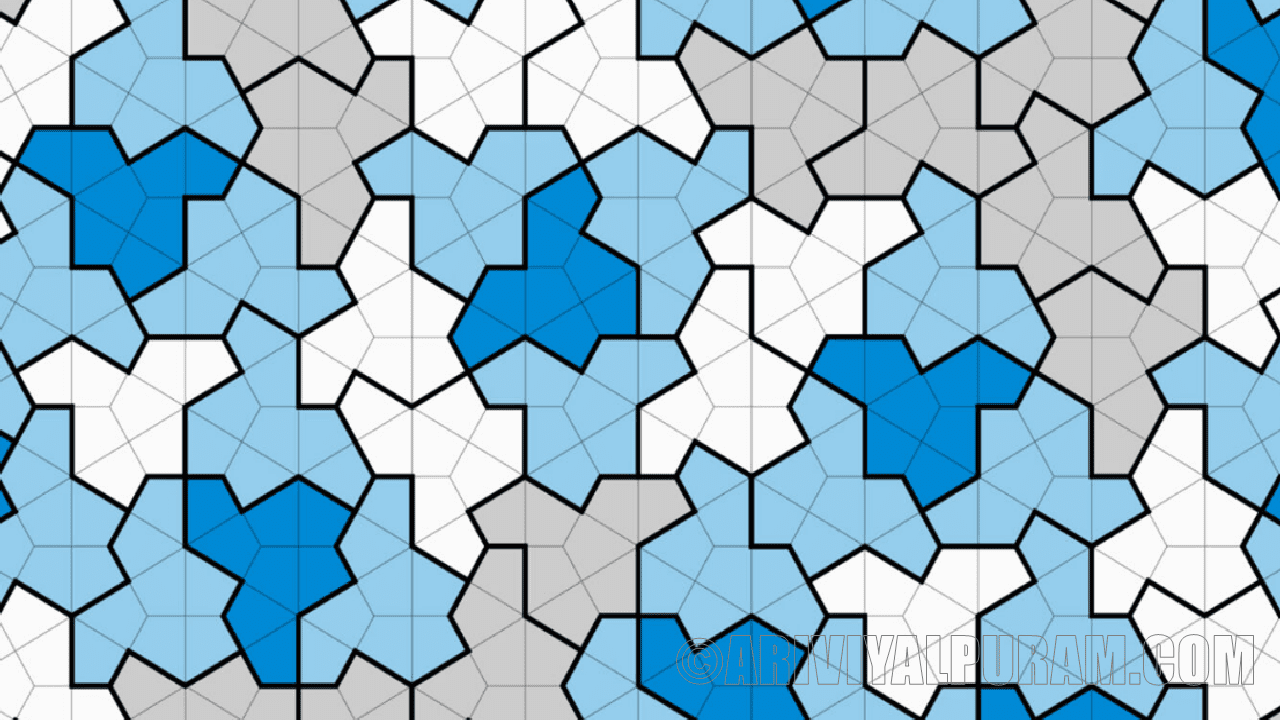
ஸ்மித்தும் சகாக்களும் ஓடு ஒரு ஐன்ஸ்டீன் என்பதை இரண்டு வழிகளில் நிரூபித்தார்கள். தொப்பிகள் மெட்டாடைல்ஸ் எனப்படும் பெரிய கொத்துக்களாக தங்களை அமைத்துக் கொள்வதை ஒருவர் கவனித்ததில் இருந்து வந்தது. அந்த மெட்டடைல்கள் பின்னர் இன்னும் பெரிய சூப்பர்டைல்களாகவும், மேலும் காலவரையின்றி, ஒரு வகை படிநிலை அமைப்பில் ஒழுங்கமைக்கப்படுகின்றன, இது அவ்வப்போது அல்லாத டைலிங்ஸுக்கு பொதுவானது. இந்த அணுகுமுறையானது தொப்பி டைலிங் முழு எல்லையற்ற விமானத்தையும் நிரப்ப முடியும் என்பதையும், அதன் முறை மீண்டும் வராது என்பதையும் வெளிப்படுத்தியது.
இரண்டாவது ஆதாரம், தொப்பியானது தொடர்ச்சியான வடிவங்களின் ஒரு பகுதியாகும் என்ற உண்மையை நம்பியிருந்தது. தொப்பியின் பக்கங்களின் ஒப்பீட்டு நீளத்தை படிப்படியாக மாற்றுவதன் மூலம், கணிதவியலாளர்கள் ஒரே மாதிரியான திரும்பத் திரும்பக் கிடைக்காத ஓடுகளின் குடும்பத்தை உருவாக்க முடிந்தது. அந்தக் குடும்பத்தின் உச்சக்கட்டத்தில் உள்ள ஓடுகளின் ஒப்பீட்டு அளவுகள் மற்றும் வடிவங்களைக் கருத்தில் கொண்டு, ஒன்று செவ்ரானைப் போலவும் மற்றொன்று வால்மீனை நினைவூட்டுவதாகவும் உள்ளது. தொப்பியை குறிப்பிட்ட கால இடைவெளியில் அமைக்க முடியாது என்பதை குழுவால் காட்ட முடிந்தது.
தாள் இன்னும் மதிப்பாய்வு செய்யப்படவில்லை என்றாலும், இந்தக் கட்டுரைக்கு நேர்காணல் செய்யப்பட்ட வல்லுநர்கள் முடிவு விரிவான ஆய்வுக்கு இருக்கக்கூடும் என்று ஒப்புக்கொள்கிறார்கள்.
திரும்பத் திரும்ப வராத வடிவங்கள் நிஜ உலக இணைப்புகளைக் கொண்டிருக்கலாம். மெட்டீரியல் விஞ்ஞானி டான் ஷெக்ட்மேன் 2011 ஆம் ஆண்டு வேதியியலுக்கான நோபல் பரிசை வென்றார், குவாசிகிரிஸ்டல்கள், அணுக்களைக் கொண்ட பொருட்கள், மீண்டும் மீண்டும் நிகழாத, பெரும்பாலும் பென்ரோஸின் டைலிங்க்களுக்கு ஒப்புமைகளாக விவரிக்கப்பட்டுள்ளன. புதிய அபிரியோடிக் ஓடு பொருள் அறிவியலில் மேலும் விசாரணைகளைத் தூண்டக்கூடும் என்று செனெச்சல் கூறுகிறார்.
இதே போன்ற ஓடுகள் கலைஞர்களை ஊக்கப்படுத்தியுள்ளன, மேலும் தொப்பியும் விதிவிலக்கல்ல என்று தோன்றுகிறது. ஏற்கனவே டைலிங் சிரிக்கும் ஆமைகள் மற்றும் சட்டைகள் மற்றும் தொப்பிகளின் ஜம்பல் என கலைநயத்துடன் வழங்கப்பட்டுள்ளது. கூடுதல் ஐன்ஸ்டீன்களுக்கான வேட்டையை ஆராய்ச்சியாளர்கள் தொடர வேண்டும் என்று கனடாவில் உள்ள வாட்டர்லூ பல்கலைக்கழகத்தின் கணினி விஞ்ஞானி கிரேக் கப்லான் கூறுகிறார். “இப்போது நாங்கள் கதவைத் திறந்துவிட்டோம், மற்ற புதிய வடிவங்கள் வரும் என்று நம்புகிறேன்” என் விஞ்ஞானிகள் கூறுகின்றனர்.